
El número de oro, la proporción áurea, la sección dorada, Φ – φ
(phi en griego), son algunos de los nombres con los que se ha conocido a
este enigmático número irracional, al cual se le ha creado un sinfín de
mitos y también se ha descubierto una inconmensurable presencia en la
naturaleza, arte y arquitectura.
En las siguientes secciones trataremos de mostrar todos los aspectos
importantes relacionados a la divina proporción y porqué termina siendo
una herramienta útil para el diseño.
Se cree que la proporción dorada estuvo presente en la arquitectura y escultura Babilónica, Asiria y Egipcia sin embargo, no existe prueba fehaciente de ninguna de estas alegaciones. La primera vez que se tiene registro de esta misteriosa proporción es con el matemático griego Euclídes (325 a. C. - 2 5 a. C.).

Avanzando en la historia hacia la época del renacimiento, el matemático y teólogo Luca Pacioli (1445 - 1517), uno de los maestros de matemáticas del gran Leonardo DaVinci, publicar a “La divina proporción” en 1509. En dicho trabajo enumera 5 razones por las cuales debe ser considerado 'divino' al número de oro:

El matemático alemán y reconocido astrónomo Johaness Kepler, famoso por sus leyes sobre el movimiento de los planetas en su órbita al rededor del Sol, dejó su apreciación acerca de la proporción áurea en uno de sus libros de la siguiente manera:
Otro matemático alemán de nombre Martin Ohm (1792 - 1872), es el primero en acuñar el término “sección dorada” al referirse a ésta proporción en la segunda edición de su libro “Las matemáticas puras elementales” en 1835.
Hasta el siglo XIX era frecuente el uso de la letra griega τ (tau) al referirse a esta proporción, ésto viene de que se usaba la palabra τομή, que en griego significa ‘sección’, sin embargo esta proporción y sus derivados se pueden extrapolar a distintos usos más allá de referirse a secciones geométricas, es por ésto que a principios del siglo XX el matemático estadounidense Mark Barr realiza el cambio a la letra griega (phi) Φ en mayúscula que es φ en minúscula.

La arbitraria elección de esta letra griega se debe a que es la primera letra del nombre del más famoso de los escultores de la antigua Grecia, Fidias (500 a. C. - 431 a. C. -fechas en debate), cuyo nombre en griego es Φειδίας, a éste se le atribuyen algunas de las obras más bellas de la historia, incluso una de las 7 Maravillas del Mundo Antiguo. Se dice que Fidias utilizaba recurrentemente el número de oro para la elaboración de sus obras maestras, por más que no existe constancia certera de que ésto haya sido de esta manera, es en su honor que se eligió la letra Φ – φ.
Si bien la palabra matemáticas muchas veces genera una barrera mental, se intentó resumir de la forma más clara los conceptos necesarios relacionados a φ para efectos de éste sitio web.
Es la base y se refiere a la interpretación del griego Euclídes, donde una línea está dividida en su punto de oro cuando la sección corta en comparación a la sección grande es proporcionalmente igual a la comparación de la sección grande con la línea entera. Esperamos que el siguiente gráfico lo ilustre más fácilmente:
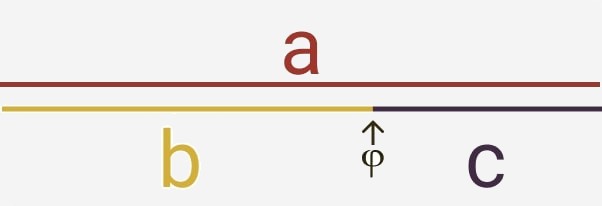

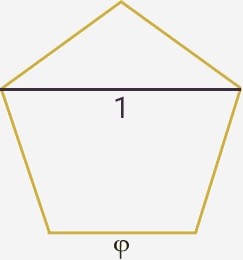
De ésta manera si consideramos la línea entera con una longitud de 1 unidad , la sección donde se cumple ésta regla previamente descrita solamente puede encontrarse en el punto 0.6180339 ....
Se considera otra cara de la misma moneda. Ésta secuencia, si bien se rastrea su aparición a las matemáticas de la India en los primeros siglos d.C. En realidad se la conoce mundialmente gracias a Leonardo de Pisa, más conocido como Fibonacci (1170 – 1240).
Es una secuencia sencilla que empieza por 0 y 1, se suman estos dos números y luego se suma el resultado con el último número de la secuencia, así sucesivamente...
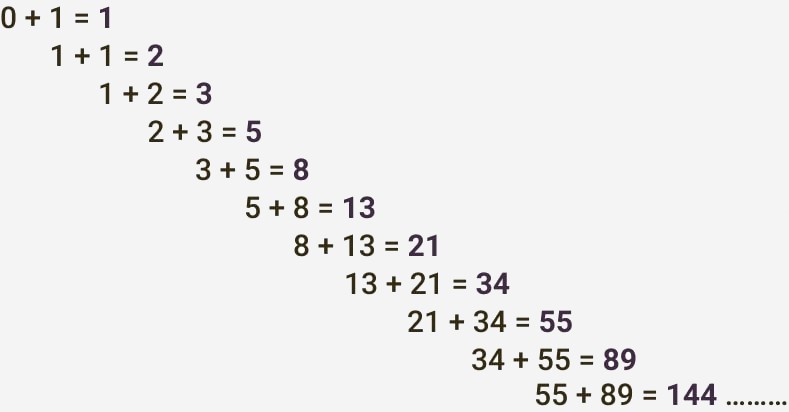
Si elegimos un número de la secuencia de Fibonacci y lo dividimos entre su inmediato antecesor, el resultado se va acercando a φ a medida que hacemos ésta operación con números más altos, ejemplificando:
21 / 13 = 1.61538...
144 / 89 = 1.617977...
1597 / 978 = 1.618034...
De igual forma la obtención de un número de Fibonacci
cualquiera puede inferirse a través de una operación
matemática en base a φ:
Fn = 1/5 [φn–(1 - φ)n]
Es por estas similitudes que transfiriendo los números de la secuencia de Fibonacci a diámetros de círculos o lados de cuadrados tenemos figuras cuyas proporciones entre sí son las del número de oro. Ésto se explica mejor en la sección de Geometría
Curiosamente... una propiedad destacable numéricamente es que tanto φ2, φ y 1/φ tienen exactamente los mismos infinitos decimales.
φ2 = 2.6180339...
φ = 1.6180339...
1/φ = 0.6180339...
Otra forma de destacar ésta propiedad, tenemos que φ es el único número (racional o irracional) que solo con sumarle el número 1 ya obtenemos su cuadrado. φ2 = φ + 1
Para formar un rectángulo áureo a partir de una línea donde se haya encontrado su punto de oro, es simplemente tomar la sección más grande y colocarla en el vértice perpendicularmente respecto a la línea entera y completar el rectángulo.
Al trazar una línea perpendicular dentro el rectángulo y exactamente en el punto φ, tendríamos un cuadrado con cada lado del tamaño de la sección grande y encuentra a lado su otro punto rectángulo φ en su áureo más extremo pequeño, más largo, se al cual puede si se le repetir la operación, así una y otra vez.
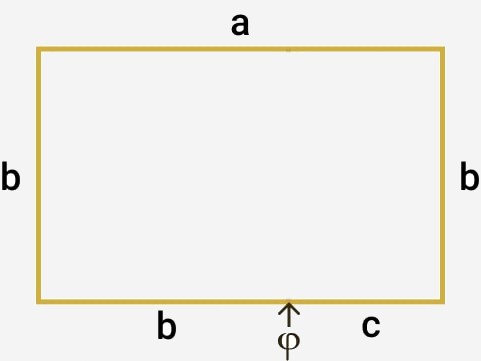
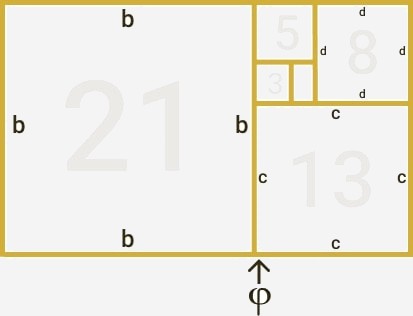
Tener un rectángulo áureo con la división en φ nos brinda la posibilidad de dividir el contenido de un elemento de manera armoniosa (más sobre ésto en la sección de “ Aplicación en diseño ” ).
Sin embargo podemos observar que se forman varios cuadrados al realizar la anterior operación. Si en determinado momento extraemos los cuadrados y al más pequeño le colocamos 1 x 1 de longitud en sus lados, tenemos que el siguiente cuadrado es de 2 x 2, el siguiente de 3 x 3, luego 5 x 5, 8 x 8, 13 x 13, 21 x 21, etc. Siguiendo así la secuencia de Fibonacci.
Los círculos son un complemento al punto anterior, y es que si dentro de cada cuadrado trazamos un círculo con el diámetro igual a las longitudes de los lados del cuadrado, tenemos círculos cuyas proporciones uno de otro siguen la razón del número de oro.
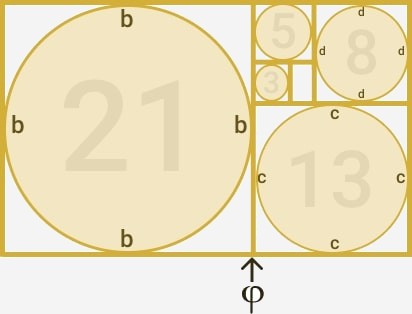
Ésto es explicado para demostrar las variaciones y utilidades que tiene manejar el concepto de la proporción áurea más allá de una simple línea o un rectángulo.

Se trata de una de las figuras más conocidas cuando se trata de φ. Así como el manejo de la sección áurea va más allá de una línea con un punto, pasa por un rectángulo proporcionalmente seccionado, se deducen cuadrados y círculos de oro, también tenemos otra figura útil que es la espiral.
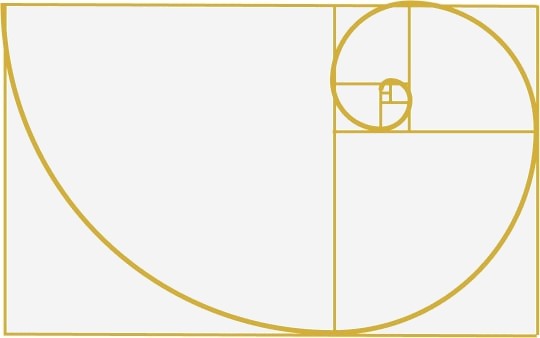
Se ha expuesto los valores más usados y de mayor interés; sin embargo, existe una gran cantidad de otras aplicaciones de esta proporción de oro dentro de la geometría.
Están los triángulos con proporción áurea, muy similar a la operación del rectángulo, con un triángulo isósceles dónde si los dos lados más extensos son de 1 unidad el más corto tiene la extensión de φ, al seccionar un lado extenso en su punto de oro y trazar una diagonal desde el vértice opuesto se forma un nuevo triángulo áureo, y así sucesivamente.
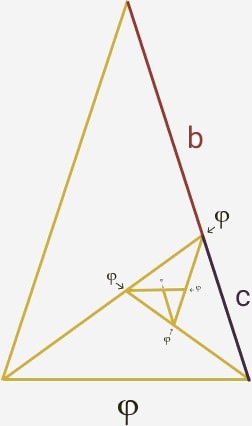
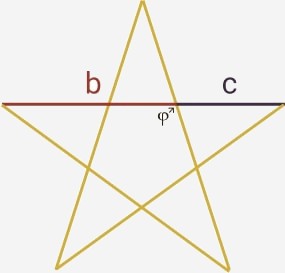
Los pentagramas, donde cada línea es intersectada en su punto φ por otra línea.
Al formarse un pentágono en su interior se crea una segunda figura con propiedades simétricas con proporción de oro, es más, si la diagonal del pentágono es de 1 unidad de longitud, cualquiera de sus lados necesariamente sería φ.
El ángulo de plata es 360° / (φ + 1) = 137.5°
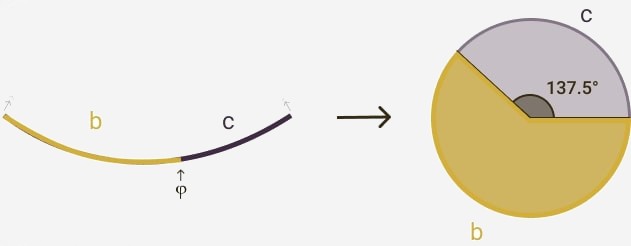
No es necesario ahondar ni mezclar más éstos y otros conceptos, simplemente sirve para encontrar varias aplicaciones respecto a diferentes formas geométricas distintas.
El número de oro está presente en diversas formas en la
naturaleza, veamos algunos ejemplos
Si Dios nos creó a su imagen y semejanza, no es de extrañarse
encontrar la proporción dorada en nuestros cuerpos.
La estatura total respecto a la distancia entre el ombligo a los
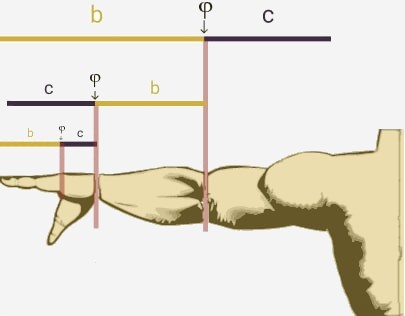
pies sigue ésta proporción, así como la distancia total del brazo
extendido, del hombro a los dedos, con el punto de oro en el codo,
también desde el codo hasta la punta de los dedos, donde φ se
encuentra en la muñeca. En otra extremidad tenemos la distancia e
la cadera a la punta de los dedos de los pies, obteniendo la
sección de oro en la rodilla.
Así también se encuentran resultados en los considerados rostros
más simétricos en los dientes incisivos, la nariz y la boca, etc.
Pero llevando a un nivel más profundo y fundamental el largo y
ancho en una vuelta de la doble hélice del ADN es de 34 y 21
ángstrom respectivamente (dos números de la secuencia de Fibonacci
y relacionados con una proporción de φ).


El resto de la naturaleza sigue ésta proporción en diversos campos, como:




Quizás éste vídeo pueda ser más ilustrativo a lo mencionado:
Vale decir, que la naturaleza del cosmos y la vida es sumamente variada y compleja, intervienen un sinnúmero de variables y tenemos una infinidad de entidades, tanto en plantas, animales o cosas inanimadas. Las reglas previamente descritas no necesariamente tienen que aplicarse a todas las especies y contamos con ejemplos de diferentes tipos (más sobre la desmitificación en conclusiones).
Desde su definición y establecimiento, la proporción áurea ha sido
de uso frecuente en el arte, ya sea en pintura, escultura,
arquitectura e incluso en música.
Respecto a este último arte, podemos decir que la secuencia de
Fibonacci es fundamental para la música, tenemos:
En las piezas musicales de Mozart, Beethoven, Bach y otros grandes
artistas, se puede encontrar tanto la proporción áurea en la
división de sus compases, como la serie de Fibonacci y la
partitura de secciones.
Por ser visualmente más fácil de reconocer, la aparición de φ
en diversas maneras ha estado presente en la pintura desde tiempos
antiguos. Vale mencionar que la utilización de la sección dorada
no es una regla estricta y sirve primordialmente como guía de
proporciones, es decir, determinada parte de una pintura no tiene
que pasar exactamente por la línea, el punto o la espiral, o si
quiera ser una forma recta.
Tenemos una diversidad de cuadros, desde DaVinci, Micheangelo,
Dalí, Durero, Sandro Botticelli, entre los más conocidos.


En cuanto a la escultura, varias de las mejores obras de la humanidad, como el David de Michelangelo, Venus de Milo de Alejandro de Antioquía, o el busto de Nefertiti en el antiguo Egipto, tienen la proporción áurea sus dimensiones. Más reciente tenemos “La vida y la Flor de Vida” de Ibo Bonilla en Costa Rica.

La arquitectura ha sido un punto interesante respecto a la
utilización de la sección de oro, desde quienes afirman que la
pirámide de Keops construida hace 4 600 años tiene proporciones de
oro en su altura, base y caras.
De igual forma se atribuye el uso de φ a Fidias, en la
creación del Partenón en Atenas. Tenemos a la proporción áurea en
Notre Dame, la torre Eiffel, el Taj Mahal, entre las estructuras
antiguas más famosas, ya en la actualidad existe una gran cantidad
de edificios construidos con esta proporción, como “The CN Tower”
en Canadá.


Si bien la matemática, historia y presencia en la naturaleza es
sumamente interesante e intrigante. Para nosotros y en la
actualidad lo más importante es la aplicabilidad en el diseño.
Existen varias maneras de aplicar φ en un diseño, desde la
disposición en elementos, el logo o incluso el tamaño de la
fuente.
Respecto a éste último, la manera de proceder es utilizando la
proporción entre distintos tamaños de letras y espacios entre
líneas, para mantener un aspecto armonioso.

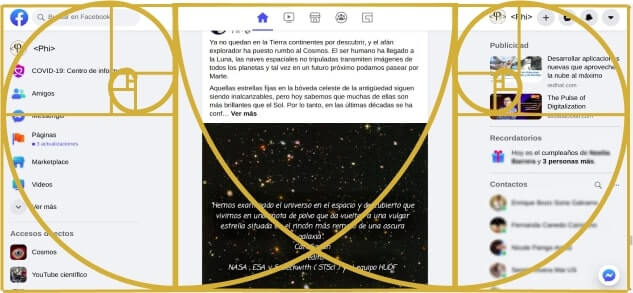
Seguir con la proporción dorada en la disposición de elementos es lo común cuando se analiza el arte de la pintura y podemos extrapolar este concepto al diseño de una web por ejemplo. La manera más reconocible de hacerlo es en la definición de las proporciones para el contenido, fijando el ”sidebar” o contenido secundario en la sección más corta, como el siguiente ejemplo:

La manera más frecuente en la que se usa la proporción áurea y que no tenemos mucha consciencia al verla, es en los logotipos. Las marcas más reconocidas del mundo aprendieron a utilizar ésta propiedad armoniosa en sus logos, ya sea solo en la proporción de línea recta, con el rectángulo, cuadrado, círculos o espiral dorada. Mejor vemos los siguientes ejemplos en práctica:

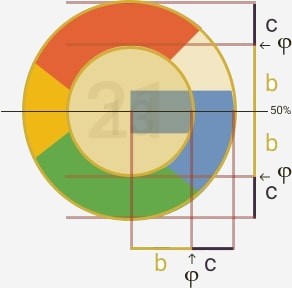

De esta manera podemos observar que la presencia de la proporción áurea resulta ser muy importante y esta presente en todos los aspectos de un diseño armonioso.
Si bien, parecería que el número de oro es “mágico” y divino sin explicación, así como parecería estar literalmente en todo. Ninguna de éstas afirmaciones es cierta, la investigación y conocimiento a profundad de la proporción de oro nos lleva a las siguientes conclusiones.

En muchos casos no se tiene certeza de que un autor la haya utilizado a propósito la proporción áurea, por ejemplo, si bien los dedos de Adán y Dios, en la famosísima obra de Micheangelo están exactamente en la sección de oro, no hay ningún registro de que lo realizó con φ en mente. Es lo mismo para construcciones como el Partenón o la Gran Pirámide de Guiza, ningún registro que lo corrobore, podría ser que simplemente se diseñaron con distintos requerimientos en mente y coincide con la proporción dorada, simplemente porque resulta ser más eficiente (más sobre ésto en los siguientes párrafos).

De todas maneras respecto a éstas y otras construcciones, faltan elementos y se desconoce el tamaño real u original para un cálculo preciso pues se falla por ciertos decimales.
Otra conclusión con la que hay que luchar constantemente es el llamado “efecto Baader-Meinhof”, o la “ilusión por frecuencia”, nuestro cerebro ha evolucionado para premiar los patrones, por lo cual cuando tenemos nueva información acerca de un patrón interesante y sorprendente, solemos tratar de verlo en todo lado.
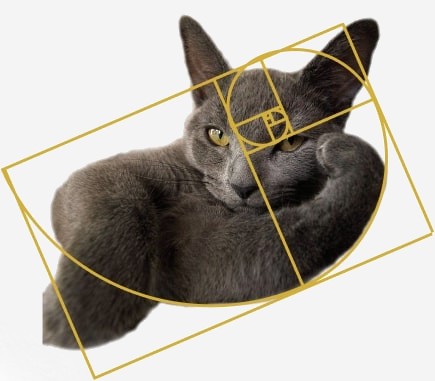
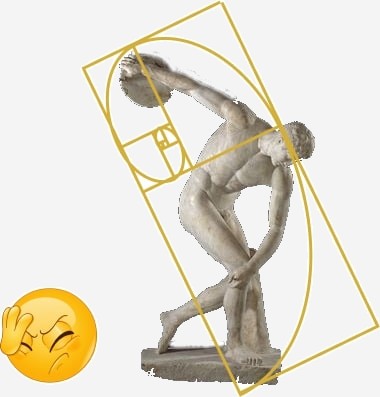
Ésto se demuestra como fue mencionado previamente, ya que existen galaxias en espiral, cuernos de carnero, cefalópodos o caracoles que no cumplen con la espiral de oro, por más que se intente forzarla. Al igual que pinturas o esculturas donde se trata de introducir un rectángulo áureo donde simplemente no hay, y probablemente no era necesario.
Pero y en la naturaleza? Hay muchos e intensos ejemplos... Pues sencillamente la respuesta es que la naturaleza es floja...... Para absorber la mayor cantidad de recursos, invertir la menor cantidad de energía y realizar las tareas de la forma más eficiente, la naturaleza necesita un ángulo no repetitivo, una distribución eficaz o el movimiento más simple.
Es por ésto que las raíces en una semilla emergen en una espiral logarítmica para aprovechar mayor cantidad de agua sin perjudicar a la otra raíz. Las flores desarrollan la cantidad mínima de pétalos para la mayor exposición eficiente al sol y ésto solo puede darse siguiendo la secuencia de Fibonacci. El vuelo del halcón para agarrar a su presa al darse en la espiral dorada le da el mayor rango de visión con el menor esfuerzo posible.

De ésta manera la naturaleza realiza el uso de φ, no tiene relación con la ‘belleza’, sino con la eficiencia, sin embargo, nosotros los seres humanos hemos evolucionado en la naturaleza donde el reconocimiento de patrones es útil. Endiosamos la simetría y ya sea subconscientemente o no, tenemos a la proporción dorada como un elemento armonioso.
Importante destacar, que en ningún sentido la regla de oro es una norma inquebrantable, ni en la naturaleza ni en el arte, sino meramente una guía de disposición que se puede ser o no útil dependiendo de la obra.
Pero final uno no desarrolla su logo porque la pirámide de Keops haya o no sido diseñada con φ, uno no distribuye el contenido de su sitio web porque DaVinci haya usado φ para hacer la Monalisa....
Se usa tanto por demostrar su simetría en la mente y más importante, porque es la corriente que se sigue actualmente aunque no nos demos cuenta, la usan todas las grandes marcas y es una guía sencilla para llegar a ser armonioso con el menor esfuerzo, agradando fácilmente a la vista.
